Category Archives: 01 Mathematics

Matrices, Scalars, Vectors and Vector Calculus 3

by ateixeira

After introducing some mathematical machinery with our first and second posts it is now time for us to look into some Newtonian Physics, after a brief look into vector integration.

— 1. Vector Integration —

When dealing with vectors and the mathematical operation we have three basic options:

  • Volume integration
  • Surface integration
  • Line (contour) integration

The result of integrating a vector, {\vec{A}=\vec{A}(x_i)}, over a volume is also a vector and the result is given by the following expression:

\displaystyle \int_V \vec{A}dv = \left( \int_V A_1 dv, \int_V A_2 dv, \int_V A_3 dv \right) \ \ \ \ \ (1)

Hence, the result of vector integration is just three separate integration operations (one of each spatial dimension).

The result of integrating the projection of a vector {\vec{A}=\vec{A}(x_1)} over an area is what is called surface integration.

Surface integration is always done with the normal component of {\vec{A}} over the surface {S} in question. Thus what we need to define first is the normal of a surface at a given point. {d\vec{a}=\vec{n}da} will be this normal. We still have the ambiguity of having two possible directions for the normal at any given point, but this is taken care of by defining the normal to be on the outward direction of a closed surface.

Hence the quantity of interest is {\vec{A}\cdot d\vec{a}=\vec{A}\cdot \vec{n} da} ({da_1=dx_2dx_3} for example) with

\displaystyle \int_S \vec{A}\cdot d\vec{a} = \int_S \vec{A}\cdot \vec{n}da \ \ \ \ \ (2)

As for the line integral it is define along the path between two points {B} and {C}. Again we have to consider the normal of {\vec{A}=\vec{A}(x_i)}, but this time the quantity of interest is:

\displaystyle \int_{BC} \vec{A}\cdot d\vec{s} \ \ \ \ \ (3)

The quantity {d\vec{s}} is an element of length along {BC} and is taken to be positive along the direction in which the path is defined.

Matrices, Scalars, Vectors and Vector Calculus 2

by ateixeira

In the last post we took our first step in the mathematical introduction to classical Mechanics. In this post we’ll introduce a few physical concepts and some more mathematical tools.

— 1. Velocity and Acceleration —

The first thing to notice is that in Physics velocity is a vector concept. That means that in order for us to specify the velocity of an entity we must not only indicate its magnitude but also its direction.

First of we need to define a frame.

Definition 1

A frame is a set of axis and a special point that is taken as the origin that allows one to describe the motion of a particle.

When to get to real Physics we’ll talk a little bit more of what is a particle in Physics but for now we’ll just leave it to intuition and/or background knowledge.

If we trace the position of a particle for a given period of time what we get is curve whose parameter is time and this curve has the name of trajectory.

If we want to keep track of the variations of the position of a particle when it is describing a given trajectory we can do that using the concept of displacement.

Definition 2 Displacement is the difference between the final and initial positions of a particle. It is represented by the symbol 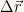{\Delta\vec{r}} and is calculated in the following way:

\displaystyle \Delta\vec{r}=\vec{r}_f - \vec{r}_i \ \ \ \ \ (1)

Now we all know that when a body describes a trajectory some parts of it may take a longer time and others a shorter time. To rigorously describe the notion of a particle we have to take into account its variability in the motion and we do this by introducing the concept of velocity.

Definition 3

The average velocity of a particle is the rate of change in position of a particle for a given time interval.

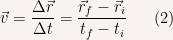
\displaystyle \vec{v}=\frac{\Delta\vec{r}}{\Delta t}=\frac{\vec{r}_f - \vec{r}_i}{t_f-t_i} \ \ \ \ \ (2)

 
Definition 4

Sometimes we aren’t interested in the average velocity and we want to know what is the velocity of a particle in a given instant. Intuitively we know that if we measure the average velocity in a sufficiently small interval we won’t be making a very big error in determining the value of the velocity.

If we let the time interval go to to zero what the have is the velocity of the particle for the instant considered. We can be rest assured that such a limit always exist since we are dealing with real bodies and their movements are always smooth.

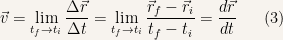
\displaystyle \vec{v}=\lim_{t_f \rightarrow t_i}\frac{\Delta\vec{r}}{\Delta t}=\lim_{t_f \rightarrow t_i}\frac{\vec{r}_f - \vec{r}_i}{t_f-t_i}=\frac{d\vec{r}}{dt} \ \ \ \ \ (3)

 

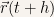Another way to mathematically define the average velocity and velocity is to make a change of variable and define {h=t_f-t_i} and calculate {\vec{r}(t)}, {\vec{r}(t+h)} and {\lim_{h \rightarrow 0}}.

The other quantity of physical interest is average acceleration and it is the the rate of change in velocity of a particle in a given time interval.

The definitions are analogous to the ones of average velocity and we just have to change 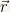{\vec{r}} to {\vec{v}}.

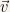We’ll just state the equation for acceleration here:

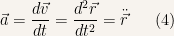
\displaystyle \vec{a}=\dfrac{d\vec{v}}{dt}=\frac{d^2\vec{r}}{dt^2}=\ddot{\vec{r}} \ \ \ \ \ (4)

 

Where 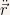{\ddot{\vec{r}}} is the so called Newton notation and indicates that we are differentiating 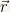{\vec{r}} two times with respect to 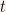{t}. Obviously that one dot indicates that we are differentiating one time, and etc.

If we use Cartesian coordinates we know that it is 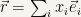{\vec{r}=\sum_i x_i\vec{e}_i}. Since our basis vectors are fixed it follows that 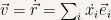{\vec{v}=\dot{\vec{r}}=\sum_i \dot{x_i}\vec{e}_i} and that {\vec{a}=\dot{\vec{v}}=\sum_i \ddot{x_i}\vec{e}_i}.

— 2. Curvilinear Coordinates —

Sometimes to use Cartesian Coordinates in order to describe the motion of a particle is very awkward and one instead uses some other kind of curvilinear coordinates. The ones that are most used are, polar coordinates, cylindrical coordinates and spherical coordinates.

— 2.1. Polar Coordinates —

If we are dealing with two dimensional problems that have circular symmetry then the best way to deal with them is to use polar coordinates.

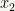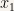In this system of coordinates instead of the {_1x} and {x_2} coordinates, one uses a radial coordinate {r} that expresses the distance that a point is from the origin and an angular coordinate {\theta}. This angular coordinate is measured from the {x_1} axis to the position vector in counter clockwise direction.

The range of values for these two variables are 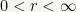{0<r<\infty} and {0\leq \theta \leq 2\pi}. Notice that in {r=0} {\theta} isn’t defined and thus the origin can be thought to be a kind of singularity, but this is only so because we chose a particular set of coordinate and it isn’t intrinsic to the point itself.

As indicated in the picture the transformation of coordinates is:

  • {x_1=r \cos \theta}
  • {x_2=r \sin \theta}
  • {\theta=\arctan \left(\dfrac{x_2}{x_1}\right)}

— 2.2. Cylindrical Coordinates —

Sometimes when dealing with three dimensional problems we have to deal with circular symmetry around a certain axis. If this happens the most apt way to deal with the said problem is to use cylindrical coordinates.

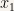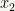Again we’ll use a mix of radial distances and angular distances. First we’ll only think about the plane formed by the {x_1} and {x_2} axes. In this plane we’ll project the position vector of a given point. The angle between 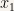{x_1} and this projection is {\theta}. The other two coordinates are {r} which is the distance between the point in question and the origin, and {x_3} (or {z}).

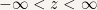The range of values for these three coordinates are {0 < r < \infty}, {0\leq \theta \leq 2\pi} and {-\infty < z < \infty},

As indicated in the pictures the transformation of coordinates is:

  • {x_1=r \cos \theta}
  • {x_2=r \sin \theta}
  • {x_3=z}

— 2.3. Spherical Coordinates —

The last kind of curvilinear coordinates that we’ll look at are spherical coordinates. This kind of coordinates are extremely useful when a problem has spherical symmetry.

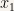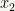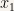This time we’ll have one radial coordinate and two angular coordinate. Like we did for cylindrical coordinates first we’ll project the position vector into the {x_1}, {x_2} plane and define {\phi} to be the angle between {x_1} and the projection of the position vector. {r} is the distance between the origin and the point in question. The second angular coordinate is {\theta} and it is measured between {x_3} and the position vector.

As can be seen from the picture the change of variables from spherical coordinates to Cartesian coordinates is:

  • {x_1=r \sin \theta \cos \phi}
  • {x_2=r \sin \theta \sin \phi}
  • {x_3=r \cos \theta}

The range of each coordinate is defined to be {0 < r < \infty}, {0 \leq \phi \leq 2\phi} and {0 \leq \theta \leq \pi}.

— 3. Velocity and Acceleration in Curvilinear Coordinates —

Having defined the previous three systems of coordinates it is time for us to know how to write the velocity and acceleration of a particle in these systems of coordinates.

As we already saw for Cartesian coordinates one has the following relationships:

  • {ds^2=dx_1^2+dx_2^2+dx_3^2}
  • {v^2=\dot{x}_1^2+\dot{x}_2^2+\dot{x}_3^2}
  • {v=\dot{x}_1\vec{e}_1+\dot{x}_2\vec{e}_2+\dot{x}_3\vec{e}_3}

Our task will be to see how these equations translate when we are dealing with polar, cylindrical and spherical coordinates.

— 3.1. Polar Coordinates —

Has stated previously when we are using curvilinear coordinates the basis vector change from point to point. Hence one has to use Leibniz rule when calculating derivatives.

If we have two points that are infinitely close to each other, {P^1} and {P^2} (the reason for using superscripts will be evident right away) the infinitesimal variation in {\vec{e}_r} is {d\vec{r}_r=\vec{e}_r^2-\vec{e}_r^1} and for the angular infinitesimal variation it is {d\vec{e}_\theta=\vec{e}_\theta^2-\vec{e}_\theta^1}

The previous relationships allows one to see that the infinitesimal variation for {\vec{e}_r} is perpendicular to {\vec{e}_r} and that the infinitesimal variation for 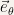{\vec{e}_\theta} is perpendicular to 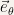{\vec{e}_\theta}. One can show this rigorously but I’ll only state the result that it is

  • {d\vec{e}_r=d\theta\vec{e}_\theta}
  • {d\vec{e}_\theta=-d\theta\vec{e}_r}

Hence

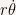{\begin{aligned} \vec{v} &=\dfrac{d\vec{r}}{dt}\\ &=\dfrac{d}{dt}\left( r\vec{e}_r \right)\\ &= \dot{r}\vec{e}_r+r\dot{\vec{e}}_r\\ &= \dot{r}\vec{e}_r+r\dot{\theta}\vec{e}_\theta \end{aligned}}

Thus the velocity can be thought has having a radial component and an angular component. The radial component is {\dot{r}} and is a measure for the variation of velocity in magnitude. The radial component is {r\dot{\theta}} and it measures the rate of change in direction for the position vector.

The {\dot{\theta}} term is so important and appears so many times that it deserves its own special name. It called the angular velocity, it is represented by the symbol {\omega} and if one is interested in an vector representation it is {\vec{v}=\vec{\omega}\times \vec{r}}.

For the acceleration it is

{\begin{aligned} \vec{a} &= \dfrac{d}{dt}\left( \dot{r}\vec{e}_r+r\dot{\theta}\vec{e}_\theta \right)\\ &= (\ddot{r}-r\dot{\theta}^2)\vec{e}_r+(r\ddot{\theta}+2\dot{r}\dot{\theta})\vec{e}_\theta \end{aligned}}

Hence the radial component of the acceleration is 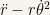{\ddot{r}-r\dot{\theta}^2} and the angular component is {r\ddot{\theta}+2\dot{r}\dot{\theta}}.

— 3.2. Cylindrical Coordinates —

For cylindrical coordinates the infinitesimal line element is 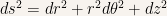{ds^2=dr^2+r^2d\theta^2+dz^2}. Hence one can show that it is

  • {v^2=\dot{r}^2+r^2\dot{\theta}^2+\dot{z}^2}
  • {\vec{v}=\dot{r}\vec{e}_r+r\dot{\theta}\vec{e}_\theta+\dot{z}\vec{e}_z}

— 3.3. Spherical Coordinates —

For spherical coordinates the infinitesimal line element is {ds^2=dr^2+r^2d\theta^2+r^2\sin ^2 \theta d\phi ^2}. And for the velocity it is

  • {v^2=\dot{r}^2+r^2\dot{\theta}^2+r^2 \sin ^2 \theta \dot{\phi}^2}
  • {\vec{v}=\dot{r}\vec{e}_r+r\dot{\theta}\vec{e}_\theta+r\sin \theta \dot{\phi}\vec{e}_\phi}

— 4. Vector Calculus —

In this part of our post we’ll take a very brief look at some concepts of vector calculus that are useful to Physics.

— 4.1. Gradient, Divergence and Curl —

If one has {\varphi=\varphi(x_1,x_2,x_3)} a scalar function, continuous and differentiable, it is by definition {\varphi'(x_1',x_2',x_3')=\varphi(x_1,x_2,x_3)}. From this it follows

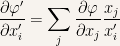
\displaystyle \frac{\partial \varphi'}{\partial x_i'}=\sum_j \frac{\partial \varphi}{\partial x_j }\frac{x_j}{x_i'}

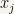The inverse coordinate transformation is {x_j= \displaystyle \sum _k\lambda_{kj}x'_k}. If we calculate the derivative of {x_j} with respect to {x_i'} it is

{\begin{aligned} \dfrac{\partial x_j}{\partial x_i'} &= \dfrac{\partial}{\partial x'_i}\left( \displaystyle \sum _k\lambda_{kj}x'_k \right)\\ &= \displaystyle \sum _k\lambda_{kj}\dfrac{\partial x'_k}{\partial x_i'}\\ &= \displaystyle \sum _k\lambda_{kj}\delta_{ik}\\ &=\lambda_{ij} \end{aligned}}

Hence it is {\displaystyle \frac{\partial \varphi'}{\partial x_i'}=\sum_j \lambda_{ij}\frac{\partial \varphi}{\partial x_j }}. From what we’ve seen in the last post this means that the function {\dfrac{\partial \varphi}{\partial x_j}} is the j-th component of a vector.

If we introduce the operator {\nabla} (sometimes called del) whose definition is

\displaystyle \nabla= \left( \frac{\partial}{\partial x_1},\frac{\partial}{\partial x_2}, \frac{\partial}{\partial x_3} \right)= \sum_i \vec{e}_i \frac{\partial}{\partial x_i}

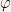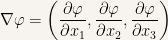we can define the gradient of a scalar function, {\varphi} to be {\nabla\varphi=\left( \dfrac{\partial \varphi}{\partial x_1},\dfrac{\partial \varphi}{\partial x_2}, \dfrac{\partial \varphi}{\partial x_3} \right)}.

The divergence of a vector field, 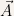{\vec{A}}, is a scalar and is defined to be:

\displaystyle \nabla\cdot\vec{A}

If the divergence of vector field is positive at a given point that means that in that point a source of the field is present. If the divergence of the field is negative that means that a sink of the field is present.

Another vector entity that one can define with the del operator is the curl of a vector field. The curl is a vector entity too and its definition is:

\displaystyle \nabla \times \vec{A}=\sum_{i,j,k}\varepsilon _{ijk}\vec{e}_i\nabla _j A_k

The last operator that we’ll define in this section is the Laplacian. This operator is the result of applying the del operator two times and it is

\displaystyle \nabla\cdot\nabla=\sum_i \frac{\partial}{\partial x_i}\frac{\partial}{\partial x_i}=\sum_i \frac{\partial ^2}{\partial x^2_i}=\nabla ^2

 

Matrices, Scalars, Vectors and Vector Calculus 1

by ateixeira

Let us imagine that we have a system of coordinates {S} and a system of coordinates {S'} that is rotated relatively to {S}. Let us consider a point {P} that has coordinates {(x_1,x_2,x_3)} on {S} and coordinates {(x'_1,x'_2,x'_3)} on {S'}.

In general it is obvious that {x'_1=x'_1(x_1,x_2,x_3)}, {x'_2=x'_2(x_1,x_2,x_3)} and that {x'_3=x'_3(x_1,x_2,x_3)}.

Since the transformation from {S} to {S'} is just a rotation we can assume that the transformation is linear. Hence we can write explicitly

{\begin{aligned} x'_1 &= \lambda _{11}x_1+ \lambda _{12}x_2 +\lambda _{13}x_3 \\ x'_2 &= \lambda _{21}x_1+ \lambda _{22}x_2 +\lambda _{23}x_3 \\ x'_3 &= \lambda _{31}x_1+ \lambda _{32}x_2 +\lambda _{33}x_3 \end{aligned}}

Another way to write the three previous equations in a more compact way is:

\displaystyle x'_i=\sum_{j=1}^3 \lambda_{ij}x_j

In case you don’t see how the previous equation is a more compact way of writing the first equations I’ll just lay out the {i=1} case.

\displaystyle x'_1=\sum_{j=1}^3 \lambda_{1j}x_j

Now all that we have to do is to sum from {j=1} to {j=3} and we get the first equation. For the other two a similar reasoning applies.

If we want to make a transformation from {S'} to {S} the inverse transformation is

\displaystyle x_i=\sum_{j=1}^3 \lambda_{ji}x'_j

The previous notation suggests that the {\lambda} indexes can be arranged in a form of a matrix:

\displaystyle \lambda= \left(\begin{array}{ccc} \lambda_{11} & \lambda_{12} & \lambda_{13} \\ \lambda_{21} & \lambda_{22} & \lambda_{23} \\ \lambda_{31} & \lambda_{32} & \lambda_{33} \end{array} \right)

In the literature the previous matrix has the name of rotation matrix or transformation matrix.

— 1. Properties of the rotation matrix —

For the transformation {x'_i=x'_i(x_i)}

\displaystyle \sum_j \lambda_{ij}\lambda_{kj}=\delta_{ik}

Where {\delta_{ik}} is a matrix known as Kronecker delta and its definition is

\displaystyle \delta_{ik}=\begin{cases} 0 \quad i\neq k\\ 1 \quad i=k \end{cases}

For the inverse transformation {x_i=x_i(x'_i)} it is

\displaystyle \sum_i \lambda_{ij}\lambda_{ik}=\delta_{jk}

The previous relationships are called orthogonality relationships.

— 2. Matrix operations, definitions and properties —

Let us represent the coordinates of a point {P} by a column vector

\displaystyle x = \left(\begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array}\right)

Using the usual notation of linear algebra we can write the transformation equations as {x'=\mathbf{\lambda} x}

Where we define the matrix product, {\mathbf{AB}=\mathbf{C}}, to be possible only when the number of columns of {\mathbf{A}} is equal to the number of rows of {\mathbf{B}}

The way to calculate a specific element of the matrix {\mathbf{C}}, we will denote this element by the symbol {\mathbf{C}_{ij}} is,

\displaystyle \mathbf{C}_{ij}=[\mathbf{AB}]_{ij}=\sum_k A_{ik}B_{kj}

Given the definition of a matrix product it should be clear that in general one has {\mathbf{AB} \neq \mathbf{BA}}

As an example let us look into;

\displaystyle \mathbf{A}=\left( \begin{array}{cc} 2 & 1\\ -1 & 3 \end{array}\right) ;\quad \mathbf{B}=\left( \begin{array}{cc} -1 & 2\\ 4 & -2 \end{array}\right)

With

\displaystyle \mathbf{AB}=\left( \begin{array}{cc} 2\times (-1)+1\times 4 & 2\times 2+1\times (-2)\\ -1\times (-1)+3\times 4 & -1\times 2+3\times (-2) \end{array}\right)=\left( \begin{array}{cc} 2 & 2\\ 13 & -8 \end{array}\right)

and

\displaystyle \mathbf{BA}=\left( \begin{array}{cc} -4 & 5\\ 10 & -2 \end{array}\right)

We’ll say that {\lambda^T} is the transposed of {\lambda} and calculate the matrix elements of the transposed matrix by {\lambda_{ij}^T=\lambda_{ji}}. In a more pedestrian way one can say that in order to obtain the transpose of a given matrix one needs only to exchange its rows and columns.

For a given matrix {\mathbf{A}} it exists another matrix {\mathbf{U}} such as {\mathbf{AU}=\mathbf{UA}=\mathbf{A}}. The matrix {\mathbf{U}} is said to be the unit matrix and usually one can represent it by {\mathbf{U}=\mathbf{1}}.

If {\mathbf{AB}=\mathbf{BA}=\mathbf{1}}, then {\mathbf{A}} and {\mathbf{B}} are said to be the inverse of each other and {\mathbf{B}=\mathbf{A}^{-1}}, {\mathbf{A}=\mathbf{B}^{-1}}.

Now for the rotation matrices it is

{\begin{aligned} \lambda \lambda ^T &= \left( \begin{array}{cc} \lambda_{11} & \lambda_{12}\\ \lambda_{21} & \lambda_{22} \end{array}\right)\left( \begin{array}{cc} \lambda_{11} & \lambda_{21}\\ \lambda_{12} & \lambda_{22} \end{array}\right) \\ &= \left( \begin{array}{cc} \lambda_{11}^2+\lambda_{22}^2 & \lambda_{11}\lambda_{21}+\lambda_{12}\lambda_{22}\\ \lambda_{21}\lambda_{11}+\lambda_{22}\lambda_{12} & \lambda_{21}^2+\lambda_{22}^2 \end{array}\right)\\ &=\left( \begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right)\\ &= \mathbf{1} \end{aligned}}

Where the second last equality follows from what we’ve seen in section 1.

Thus {\lambda ^T=\lambda ^{-1}}.

Just to finish up this section let me just mention that even though, in general, matrix multiplication isn’t commutative it still is associative. Thus {(\mathbf{AB})\mathbf{C}=\mathbf{A}(\mathbf{BC})}. Also matrix addition has just the definition one would expect. Namely {C_{ij}=A_{ij}+B_{ij}}.

If one inverts all three axes at the same time the matrix that we get is the so called inversion matrix and it is

\displaystyle \left( \begin{array}{ccc} -1 & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & -1 \end{array}\right)

Since it can be shown that rotation matrices always have their determinant equal to {1} and that the inversion matrix has a {-1} determinant we know that there isn’t any continuous transformation that maps a rotation into an inversion.

— 3. Vectors and Scalars —

In Physics quantities are either scalars or vectors (they can also be tensors but since they aren’t needed right away I’ll just pretend that they don’t exist for the time being). These two entities are defined according to their transformation properties.

Let {\lambda} be a coordinate transformation, {\displaystyle\sum_j\lambda_{ij}\lambda_{kj}=\delta_{ij}}, if it is:

  • {\displaystyle\sum_j\lambda_{ij}\varphi=\varphi} then {\varphi} is said to be a scalar.
  • {\displaystyle\sum_j\lambda_{ij}A_j=A'_i} for {A_1}, {A_2} and {A_3} then {(A_1,A_2,A_3)} is said to be a vector.

— 3.1. Operations between scalars and vectors —

I think that most people in here already know this but in the interest of a modicum of self containment I’ll just enumerate some properties of scalars and vectors.

  1. {\vec{A}+\vec{B}=\vec{B}+\vec{A}}
  2. {\vec{A}+(\vec{B}+\vec{C})=(\vec{A}+\vec{B})+\vec{C}}
  3. {\varphi+\psi=\psi+\varphi}
  4. {\varphi+(\psi+\xi)=(\varphi+\psi)+\xi}
  5. {\xi \vec{A}= \vec{B}} is a vector.
  6. {\xi \varphi=\psi} is a scalar.

As an example we will show the second proposition 5 and the reader has to show the veracity of the last proposition.

In order to show that {\xi \vec{A}= \vec{B}} is a vector we have to show that it transforms like a vector.

{\begin{aligned} B'_i &= \displaystyle\sum_j \lambda_{ij}B_j\\ &= \displaystyle\sum_j \lambda_{ij}\xi A_j\\ &= \xi\displaystyle\sum_j \lambda_{ij} A_j\\ &= \xi A'_i \end{aligned}}

Hence {\xi A} transforms like a vector.

— 4. Vector “products” —

The operations between scalars are pretty much well know by everybody, hence we won’t take a look at them, but maybe it is best for us to take a look at two operations between vectors that are crucial for our future development.

— 4.1. Scalar product —

We can construct a scalar by using two vectors. This scalar is a measure of the projection of one vector into the other. Its definition is

\displaystyle \vec{A}.\cdot\vec{B}=\sum_i A_i B_i = AB\cos (A.B)

For this operation deserve its name, one still has to prove that the result indeed is a scalar.

First one writes {A'_i=\displaystyle \sum_j\lambda_{ij}A_j} and {B'_i=\displaystyle \sum_k\lambda_{ik}B_k}, where one changes the index of the second summation because we’ll have to multiply the two quantities and that way the final result can be achieved much more easily.

Now it is

{\begin{aligned} \vec{A}'\cdot \vec{B}' &= \displaystyle\sum_i A'_i B'_i \\ &= \displaystyle \sum_i \left(\sum_j\lambda_{ij}A_j\right)\left( \sum_k\lambda_{ik}B_k \right)\\ &= \displaystyle \sum_j \sum_k \left( \sum_i \lambda_{ij}\lambda_{ik} \right)A_j B_k\\ &= \displaystyle \sum_j \left(\sum_k \delta_{jk}A_jB_k \right)\\ &= \displaystyle \sum_j A_j B_j \\ &= \vec{A}\cdot \vec{B} \end{aligned}}

Hence {\vec{A}\cdot \vec{B}} is a scalar.

— 4.2. Vector product —

First we have to introduce the permutation symbol {\varepsilon_{ijk}}. Its definition is {\varepsilon_{ijk}=0} if two or three of its indices are equal; {\varepsilon_{ijk}=1} if {i\,j\,k} is an even permutation of {123} (the even permutations are {123}, {231} and {312}); {\varepsilon_{ijk}=-1} if {i\,j\,k} is an odd permutation of {123} (the odd permutations {132}, {321} and {213}).

The vector product, {\vec{C}}, of two vectors {\vec{A}} and {\vec{B}} is denoted by {\vec{C}=\vec{A}\times \vec{B}}.

To calculate the components the components of the vector {\vec{C}} the following equation is to be used:

\displaystyle C_i=\sum_{j,k}\varepsilon_{ijk}A_j B_k

Where {\displaystyle\sum_{j,k}} is shorthand notation for {\displaystyle\sum_j\sum_k}.

As an example let us look into {C_1}

{\begin{aligned} C_1 &= \sum_{j,k}\varepsilon_{1jk}A_j B_k\\ &= \varepsilon_{123}A_2 B_3+\varepsilon_{132}A_3 B_2\\ &= A_2B_3-A_3B_2 \end{aligned}}

where we have used the definition of {\epsilon_{ijk}} throughout the reasoning.

One can also see that (this another exercise for the reader) {C_2=A_3B_1-A_1B_3} and that {C_3=A_1B_2-A_2B_1}.

If one only wants to know the magnitude of {\vec{C}} the following equation should be used {C=AB\sin (A,B)}.

After choosing the three axes that define our frame of reference one can choose as the basis of this space a set of three linearly independent vectors that have unit norm. These vectors are called unit vectors.

If we denote these vectors by {\vec{e}_i} any vector {\vec{A}} can be written as {\vec{A}=\displaystyle \sum _i \vec{e}_i A_i}. We also have that {\vec{e}_i\cdot \vec{e}_j=\delta_{ij}} and {\vec{e}_i\times \vec{e}_j=\vec{e}_k}. Another way to write the last equation is {\vec{e}_i\times \vec{e}_j=\vec{e}_k\varepsilon_{ijk}}.

— 5. Vector differentiation with respect to a scalar —

Let {\varphi} be a scalar function of {s}: {\varphi=\varphi(s)}. Since both {\varphi} and {s} are scalars we know that their transformation equations are {\varphi=\varphi '} and {s=s'}. Hence it also is {d\varphi=d\varphi '} and {ds=ds'}

Thus it follows that for differentiation it is {d\varphi/ds=d\varphi'/ds'=(d\varphi/ds)'}.

In order to define the derivative of a vector with respect to a scalar we will follow an analogous road.

We already know that it is {A'_i=\displaystyle \sum_j \lambda _{ij}A_j} hence

{\begin{aligned} \dfrac{dA'_i}{ds'} &= \dfrac{d}{ds'}\left( \displaystyle \sum_j \lambda _{ij}A_j \right)\\ &= \displaystyle \lambda _{ij}\dfrac{d A_j}{ds'}\\ &= \displaystyle \lambda _{ij}\dfrac{d A_j}{ds}\ \end{aligned}}

where the last equality follows from the fact that {s} is a scalar.

From what we saw we can write

\displaystyle \frac{d A'_i}{ds'}= \left( \frac{d A_i}{ds} \right)'=\sum_j \lambda _{ij}\frac{d A_j}{ds}

Hence {dA_j/ds} transforms like the coordinates of a vector which is the same as saying that {d\vec{A}/ds} is a vector.

The rules for differentiating vectors are:

  • {\dfrac{d}{ds}(\vec{A}+\vec{B})= \dfrac{d\vec{A}}{ds}+\dfrac{d\vec{B}}{ds}}
  • {\dfrac{d}{ds}(\vec{A}\cdot\vec{B})= \vec{A}\cdot\dfrac{d\vec{B}}{ds}+\dfrac{d\vec{A}}{ds}\cdot \vec{B}}
  • {\dfrac{d}{ds}(\vec{A}\times\vec{B})= \vec{A}\times\dfrac{d\vec{B}}{ds}+\dfrac{d\vec{A}}{ds}\times \vec{B}}
  • {\dfrac{d}{ds}(\varphi\vec{A})= \varphi\dfrac{d\vec{A}}{ds}+\dfrac{d\varphi}{ds}\vec{A}}

The proof of these rules isn’t needed in order for us to develop any kind of special skills but if the reader isn’t very used to this, then it is better for him to do them just to see how things happen.