The Wave Function Exercises 01

by ateixeira

Exercise 1

  • {<j>^2=21^2=441}

    {<j^2>=1/N\sum j^2N(J)=\dfrac{6434}{14}=459.6}

  • Calculating for each {\Delta j}
    {j} {\Delta j=j-<j>}
    14 {14-21=-7}
    15 {15-21=-6}
    16 {16-21=-5}
    22 {22-21=1}
    24 {24-21=3}
    25 {25-21=4}

    Hence for the variance it follows

    {\sigma ^2=1/N\sum (\Delta j)^2N(j)=\dfrac{260}{14}=18.6}

    Hence the standard deviation is

    \displaystyle \sigma =\sqrt{18.6}=4.3

  • {\sigma^2=<j^2>-<j>^2=459.6-441=18.6}

    And for the standard deviation it is

    \displaystyle \sigma =\sqrt{18.6}=4.3

    Which confirms the second equation for the standard deviation.

Exercise 2 Consider the first {25} digits in the decimal expansion of {\pi}.

  • What is the probability of getting each of the 10 digits assuming that one selects a digit at random.

    The first 25 digits of the decimal expansion of {\pi} are

    \displaystyle \{3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 8, 9, 7, 9, 3, 2, 3, 8, 4, 6, 2, 6, 4, 3\}

    Hence for the digits it is

    {N(0)=0} {P(0)=0}
    {N(1)=2} {P(1)=2/25}
    {N(2)=3} {P(2)=3/25}
    {N(3)=5} {P(3)=1/5}
    {N(4)=3} {P(4)=3/25}
    {N(5)=3} {P(5)=3/25}
    {N(6)=3} {P(6)=3/25}
    {N(7)=1} {P(7)=1/25}
    {N(8)=2} {P(8)=2/25}
    {N(9)=3} {P(9)=3/25}
  • The most probable digit is {5}. The median digit is {4}. The average is {\sum P(i)N(i)=4.72}.

  • {\sigma=2.47}

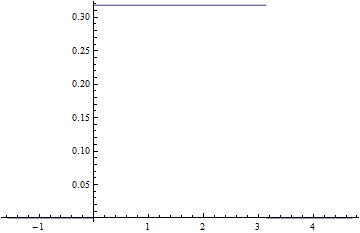
Exercise 3 The needle on a broken car is free to swing, and bounces perfectly off the pins on either end, so that if you give it a flick it is equally likely to come to rest at any angle between {0} and {\pi}.

  • Along the {\left[0,\pi\right]} interval the probability of the needle flicking an angle {d\theta} is {d\theta/\pi}. Given the definition of probability density it is {\rho(\theta)=1/\pi}.

    Additionally the probability density also needs to be normalized.

    \displaystyle \int_0^\pi \rho(\theta)d\theta=1\Leftrightarrow\int_0^\pi 1/\pi d\theta=1

    which is trivially true.

    The plot for the probability density is

    NeedleProbabilityDensity

  • Compute {\left\langle\theta \right\rangle}, {\left\langle\theta^2 \right\rangle} and {\sigma}.

    {\begin{aligned} \left\langle\theta \right\rangle &= \int_0^\pi\frac{\theta}{\pi}d\theta\\ &= \frac{1}{\pi}\int_0^\pi\theta d\theta\\ &= \frac{1}{\pi} \left[ \frac{\theta^2}{2} \right]_0^\pi\\ &= \frac{\pi}{2} \end{aligned}}

    For {\left\langle\theta^2 \right\rangle} it is

    {\begin{aligned} \left\langle\theta^2 \right\rangle &= \int_0^\pi\frac{\theta^2}{\pi}d\theta\\ &= \frac{1}{\pi} \left[ \frac{\theta^3}{3} \right]_0^\pi\\ &= \frac{\pi^2}{3} \end{aligned}}

    The variance is {\sigma^2=\left\langle\theta^2 \right\rangle-\left\langle\theta\right\rangle^2 =\dfrac{\pi^2}{3}-\dfrac{\pi^2}{4}=\dfrac{\pi^22}{12}}.

    And the standard deviation is {\sigma=\dfrac{\pi}{2\sqrt{3}}}.

  • Compute {\left\langle\sin\theta\right\rangle}, {\left\langle\cos\theta\right\rangle} and {\left\langle\cos^2\theta\right\rangle}.

    {\begin{aligned} \left\langle\sin\theta \right\rangle &= \int_0^\pi\frac{\sin\theta}{\pi}d\theta\\ &= \frac{1}{\pi}\int_0^\pi\sin\theta d\theta\\ &= \frac{1}{\pi} \left[ -\cos\theta \right]_0^\pi\\ &= \frac{2}{\pi} \end{aligned}}

    and

    {\begin{aligned} \left\langle\cos\theta \right\rangle &= \int_0^\pi\frac{\cos\theta}{\pi}d\theta\\ &= \frac{1}{\pi}\int_0^\pi\cos\theta d\theta\\ &= \frac{1}{\pi} \left[ \sin\theta \right]_0^\pi\\ &= 0 \end{aligned}}

    We’ll leave {\left\langle\cos\theta^2 \right\rangle} as an exercise for the reader. As a hint remember that {\cos^2\theta=\dfrac{1+\cos(2\theta)}{2}}.

Exercise 4

  • In exercise {1.1} it was shown that the the probability density is

    \displaystyle \rho(x)=\frac{1}{2\sqrt{hx}}

    Hence the mean value of {x} is

    {\begin{aligned} \left\langle x \right\rangle &= \int_0^h\frac{x}{2\sqrt{hx}}dx\\ &= \frac{h}{3} \end{aligned}}

    For {\left\langle x^2 \right\rangle} it is

    {\begin{aligned} \left\langle x^2 \right\rangle &= \int_0^h\frac{x}{2\sqrt{hx}}dx\\ &= \frac{1}{2\sqrt{h}}\int_0^h x^{3/2}dx\\ &= \frac{1}{2\sqrt{h}}\left[\frac{2}{5}x^{5/2} \right]_0^h\\ &= \frac{h^2}{5} \end{aligned}}

    Hence the variance is

    \displaystyle \sigma^2=\left\langle x^2 \right\rangle-\left\langle x \right\rangle^2=\frac{h^2}{5}-\frac{h^2}{9}=\frac{4}{45}h^2

    and the standard deviation is

    \displaystyle \sigma=\frac{2h}{3\sqrt{5}}

  • For the distance to the mean to be more than one standard deviation away from the average we have two alternatives. The first is the interval {\left[0,\left\langle x \right\rangle+\sigma\right]} and the second is {\left[\left\langle x \right\rangle+\sigma,h\right]}.

    Hence the total probability is the sum of these two probabilities.

    Let {P_1} denote the probability of the first interval and {P_2} denote the probability of the second interval.

    {\begin{aligned} P_1 &= \int_0^{\left\langle x \right\rangle-\sigma}\frac{1}{2\sqrt{hx}}dx\\ &= \frac{1}{2\sqrt{h}}\left[2x^{1/2} \right]_0^{\left\langle x \right\rangle-\sigma}\\ &= \frac{1}{\sqrt{h}}\sqrt{\frac{h}{3}-\frac{2h}{3\sqrt{5}}}\\ &=\sqrt{\frac{1}{3}-\frac{2}{3\sqrt{5}}} \end{aligned}}

    Now for the second interval it is

    {\begin{aligned} P_2 &= \int_{\left\langle x \right\rangle+\sigma}^h\frac{1}{2\sqrt{hx}}dx\\ &= \ldots\\ &=1-\sqrt{\frac{1}{3}+\frac{2}{3\sqrt{5}}} \end{aligned}}

    Hence the total probability {P} is {P=P_1+P_2}

    {\begin{aligned} P&=P_1+P_2\\ &= \sqrt{\frac{1}{3}-\frac{2}{3\sqrt{5}}}+1-\sqrt{\frac{1}{3}+\frac{2}{3\sqrt{5}}}\\ &\approx 0.3929 \end{aligned}}

Exercise 5 The probability density is {\rho(x)=Ae^{-\lambda(x-a)^2}}

  • Determine {A}.

    Making the change of variable {u=x-a} ({dx=du}) the normalization condition is

    {\begin{aligned} 1 &= A\int_{-\infty}^\infty e^{-\lambda u^2}du\\ &= A\sqrt{\frac{\pi}{\lambda}} \end{aligned}}

    Hence for {A} it is

    \displaystyle A=\sqrt{\frac{\lambda}{\pi}}

  • Find {\left\langle x \right\rangle}, {\left\langle x^2 \right\rangle} and {\sigma}.

    {\begin{aligned} \left\langle x \right\rangle &= \sqrt{\frac{\lambda}{\pi}}\int_{-\infty}^\infty (u+a)e^{-\lambda u^2}du\\ &= \sqrt{\frac{\lambda}{\pi}}\left(\int_{-\infty}^\infty ue^{-\lambda u^2}du+a\int_{-\infty}^\infty e^{-\lambda u^2}du \right)\\ &=\sqrt{\frac{\lambda}{\pi}}\left( 0+a\sqrt{\frac{\pi}{\lambda}} \right)\\ &= a \end{aligned}}

    If you don’t see why {\displaystyle\int_{-\infty}^\infty ue^{-\lambda u^2}du=0} check this post on my other blog.

    For {\left\langle x^2 \right\rangle} it is

    {\begin{aligned} \left\langle x^2 \right\rangle &= \sqrt{\frac{\lambda}{\pi}}\int_{-\infty}^\infty (u+a)^2e^{-\lambda u^2}du\\ &= \sqrt{\frac{\lambda}{\pi}}\left(\int_{-\infty}^\infty u^2e^{-\lambda u^2}du+2a\int_{-\infty}^\infty u e^{-\lambda u^2}du+a^2\int_{-\infty}^\infty e^{-\lambda u^2}du \right) \end{aligned}}

    Now {\displaystyle 2a\int_{-\infty}^\infty u e^{-\lambda u^2}du=0} as in the previous calculation.

    For the third term it is {\displaystyle a^2\int_{-\infty}^\infty e^{-\lambda u^2}du=a^2\sqrt{\frac{\pi}{\lambda}}}.

    The first integral is the hard one and a special technique can be employed to evaluate it.

    {\begin{aligned} \int_{-\infty}^\infty u^2e^{-\lambda u^2}du &= \int_{-\infty}^\infty-\frac{d}{d\lambda}\left( e^{-\lambda u^2} \right)du\\ &= -\frac{d}{d\lambda}\int_{-\infty}^\infty e^{-\lambda u^2}du\\ &=-\frac{d}{d\lambda}\sqrt{\frac{\pi}{\lambda}}\\ &=\frac{1}{2}\sqrt{\frac{\pi}{\lambda^3}} \end{aligned}}

    Hence it is

    {\begin{aligned} \left\langle x^2 \right\rangle &= \sqrt{\frac{\lambda}{\pi}}\int_{-\infty}^\infty (u+a)^2e^{-\lambda u^2}du\\ &= \sqrt{\frac{\lambda}{\pi}}\left(\int_{-\infty}^\infty u^2e^{-\lambda u^2}du+2a\int_{-\infty}^\infty u e^{-\lambda u^2}du+a^2\int_{-\infty}^\infty e^{-\lambda u^2}du \right)\\ &= \sqrt{\frac{\lambda}{\pi}}\left( \frac{1}{2}\sqrt{\frac{\pi}{\lambda^3}}+0+a^2\sqrt{\frac{\pi}{\lambda}} \right)\\ &=a^2+\frac{1}{2\lambda} \end{aligned}}

    The variance is

    \displaystyle \sigma^2=\left\langle x^2 \right\rangle-\left\langle x \right\rangle^2=\frac{1}{2\lambda}

    Hence the standard deviation is

    \displaystyle \sigma=\frac{1}{\sqrt{2\lambda}}

— Mathematica file —

The resolution of exercise 2 was done using some basic Mathematica code which I’ll post here hoping that it can be helpful to the readers of this blog.

// N[Pi, 25]


piexpansion = IntegerDigits[3141592653589793238462643]


digitcount = {}


For[i = 0, i <= 9, i++, AppendTo[digitcount, Count[A, i]]]


digitcount


digitprobability = {}


For[i = 0, i <= 9, i++, AppendTo[digitprobability, Count[A, i]/25]]


digitprobability


digits = {}


For[i = 0, i <= 9, i++, AppendTo[digits, i]]


digits


j = N[digits.digitprobability]


digitssquared = {}


For[i = 0, i <= 9, i++, AppendTo[digitssquared, i^2]]


digitssquared


jsquared = N[digitssquared.digitprobability]


sigmasquared = jsquared - j^2


std = Sqrt[sigmasquared]


deviations = {}


deviations = piexpansion - j


deviationssquared = (piexpansion - j)^2


variance = Mean[deviationssquared]


standarddeviation = Sqrt[variance]

Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.